Antes de tratar do método da Média Móvel é preciso apresentar a forma mais simples e até intuitiva para se realizar a previsão da demanda denominada Previsão Ingênua. Esta forma se baseia unicamente em assumir a demanda do último período como previsão para o próximo.
Por exemplo, se a demanda de sanduíches numa lanchonete escolar foi de 15 na terça-feira, assume-se que a previsão para quarta-feira será também de 15 sanduíches.
Pela simplicidade seja talvez a forma mais aplicada em situações nas quais não se tenha pessoas com conhecimentos em outros métodos de previsão.
Partindo para o método da Média Móvel, é uma forma de previsão que se utiliza de uma série temporal de dados da demanda para realizar as previsões, e consiste em realizar uma média da demanda a partir de uma quantidade de períodos pré-determinada.
Assim, determina-se uma quantidade de n períodos, e realiza-se a previsão para o período futuro t, fazendo uma média da quantidade de períodos imediatamente anteriores.
Matematicamente a equação é representada por:

A determinação da quantidade de períodos n é arbitrária, mas geralmente define-se diferentes quantidades e testa-se de modo a encontrar o valor de n que tende a ter maior aderência a demanda estudada.
Quanto maior a quantidade de períodos utilizada, maior será a suavização da demanda real. Quanto menor a quantidade de períodos mais rapidamente as previsões responderão a alterações no comportamento da demanda. Este efeito será observado posteriormente.
Considere as vendas mensais de uma pequena indústria calçadista para um de seus produtos chamado “Sapato Previllege”.
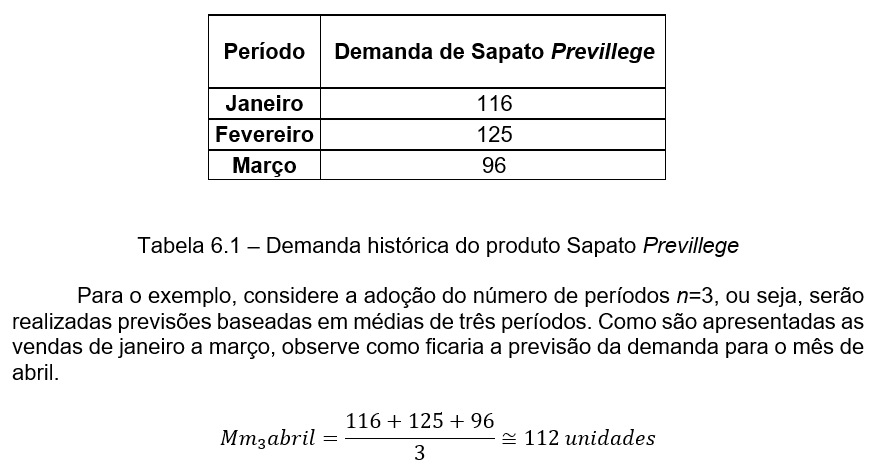
Considerando janeiro, fevereiro e março, a previsão de vendas deste produto para o mês de abril seria de 112 unidades. Aplicando este mesmo método, observe como ficariam as previsões até o mês de outubro.
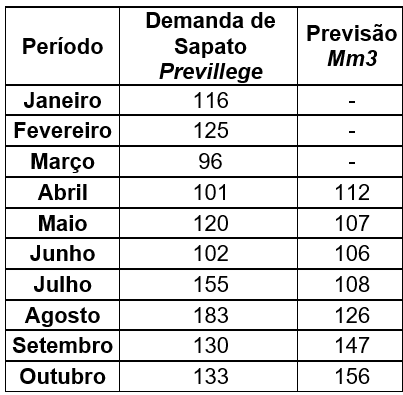
Tabela 6.2 – Previsão para Sapato Previllege com Média Móvel de 3 períodos
Como foi adotado n de três períodos para as previsões, observe que na tabela não é possível realizar a previsão para janeiro, fevereiro e março.
Por exemplo, para realizar a previsão de janeiro seria preciso as demandas dos três meses anteriores, dezembro, novembro e outubro, como estes dados não estão disponíveis pulou-se as previsões dos três primeiros meses. Normalmente, numa aplicação real seria possível buscar os dados e realizar as previsões.
No exemplo anterior, para realizar a previsão do mês de abril, utilizou-se as demandas dos meses de janeiro, fevereiro e março. Como mais um exemplo, observe o cálculo para chegar na previsão de maio, que considera as demandas de fevereiro, março e abril.
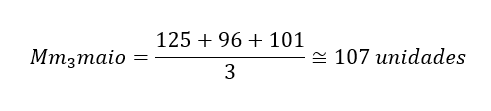
Dessa mesma forma deve-se proceder para as previsões dos períodos subsequentes, eliminando a demanda mais antiga entre as três e adicionando a próxima ao realizar a média.
À medida que as previsões são realizadas, é preciso acompanhar sua acuracidade calculando seus erros. Os erros são definidos conforme equação a seguir.
ERRO = Demanda – Previsão
Considerando
o exemplo, observe na tabela a seguir como ficariam os erros do modelo
aplicado.
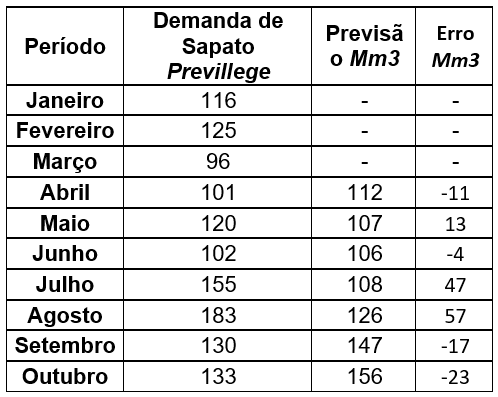
Tabela 6.3 – Erros do modelo de Média Móvel para três períodos
Como exemplo, o erro do mês de abril seria calculado da seguinte forma:
ERRO Mm3 Abr = 101 – 112 = -11
Assim, para o mês de abril o método de previsão errou -11 unidades, ou seja, sua demanda foi onze unidades menor que a previsão realizada.
Observe que ao longo dos períodos apresentados, os erros são ora positivos, ora negativos. Esta variação negativa e positiva dos erros é um comportamento completamente natural para qualquer método de previsão. Um comportamento diferente deste, ou seja, existirem somente erros positivos, ou somente erros negativos, indicam que há uma tendência persistente de aumento ou decréscimo da demanda.
Para expandir a aplicação do método, observe a tabela a seguir onde realiza-se a previsão com n=5 e n=7 períodos.
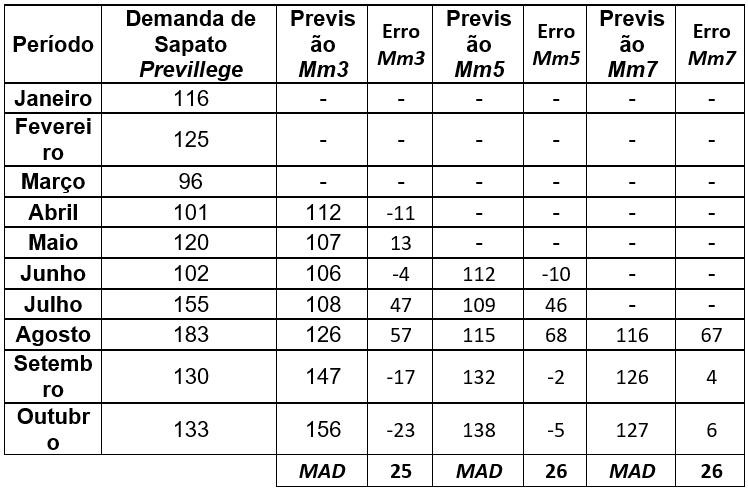
Tabela 6.4 – Previsão para 3, 5 e 7 períodos
Como exemplo, observe o cálculo para previsão do período de setembro e seu respectivo erro utilizando n=5.
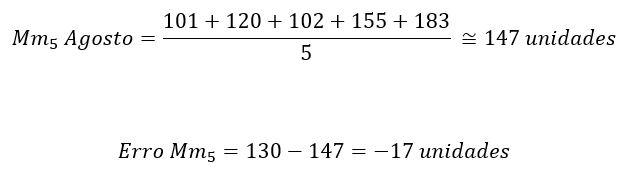
Além dos novos modelos com diferentes quantidades de períodos, na tabela também é apresentada uma nova informação que aparece com o nome MAD, do inglês Mean Absolute Deviation, em português Desvio Médio Absoluto.
O MAD é a média dos erros em módulo de cada modelo, ou seja, representa quanto em média absoluta cada modelo errou, e pode ser utilizado para fins comparativos entre eles. A equação seu cálculo é:
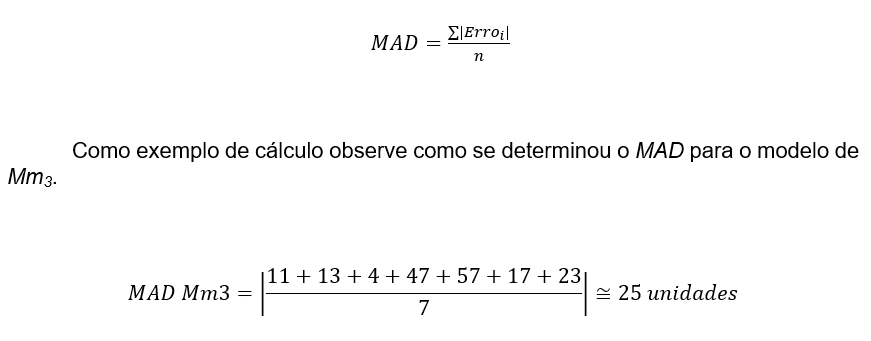
Como mencionado anteriormente, os erros das previsões tendem a se apresentarem tanto positivos como negativos, mas no cálculo do MAD, por ser em módulo, todos são considerados sem sinal.
Assim, o MAD para o modelo considerando três períodos errou em média 25 unidades em suas previsões, já os modelos com cinco e sete períodos erram coincidentemente 26 unidades.
Na comparação do MAD entre estes três modelos, cabe a ressalva que em cada um há uma quantidade diferente de períodos que foram realizadas previsões, logo, uma quantidade diferente de erros.
Aqui tomou-se a liberdade de comparar o MAD entre estes modelos porque não há dados de períodos anteriores para se fazer todas as previsões, mas na prática, o ideal é que se compare modelos com a mesma quantidade de erros observados.
Os três modelos têm erros médios muito próximos e até iguais, mas o que apresenta menor erro seria o modelo de 3 períodos, que então seria o mais indicado para se realizar estas previsões, se estes erros forem aceitáveis por parte do planejador.
Não há um consenso com relação ao que seria “um erro aceitável”, tudo dependerá do cenário analisado e a capacidade da empresa lidar com estes erros.
Por exemplo, um erro médio de 10% da demanda pode ser um erro facilmente administrável para uma determinada operação de uma empresa, mas pode não ser administrável para outra. Assim, para a primeira empresa um erro de 10% seria aceitável, já para a segunda não seria.
O ideal é que antes de se adotar o método para realização das previsões, se realize testes com diferentes valores para n, de modo a encontrar o que apresenta o menor MAD.
Dentro desta esfera, observe na figura 27.1 o comportamento das previsões em relação a demanda com a adoção de diferentes valores de n.
No gráfico são apresentadas três linhas. A linha mais espeça em preto representa o comportamento de uma demanda qualquer. Uma das linhas representa o comportamento das previsões quando se adota uma maior quantidade de períodos n na média móvel, e a outra linha representa quando se utiliza uma menor quantidade de n.
Observe o comportamento das linhas de previsão em relação a linha da demanda. A linha que representa a utilização de menos períodos tende a acompanhar de maneira mais próxima o comportamento da demanda. Quando esta sofre alterações de um período para outro, ou seja, quando a demanda diminui entre períodos a tendência dessa linha também é diminuir.
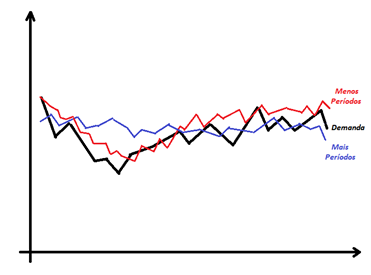
Figura 6.1 – Comportamento da previsão para diferentes números de n
Já a linha que representa maior quantidade de períodos, não acompanha a demanda tão rapidamente quando há alterações de um período para outro. Esta linha tende a ter um comportamento “mais plano”, menos errático. Ela é menos suscetível as alterações da demanda.
Em resumo, pode-se afirmar que para demanda com comportamentos mais instáveis é mais indicado adotar menores quantidade de períodos n na média móvel, e para demandas com comportamentos mais estáveis é indicado adotar maiores quantidades de períodos n.
Uma outra característica importante do método da média móvel é que com sua aplicação somente é possível realizar a previsão para um período no futuro, não é possível realizar a previsão para vários períodos a frente.
No exemplo apresentado aqui são apresentadas as demandas de todos os períodos na tabela, mas na prática os meses correm um a um. Assim, por exemplo, depois de realizar a previsão para o mês de abril, é preciso esperar que o mês de abril termine para se obter sua demanda real, e ser possível fazer a previsão para o mês seguinte, maio.
Neste material são apresentados cálculos simplificados e didáticos para compreensão do funcionamento do método, normalmente no dia a dia da atividade de planejamento ter-se-á uma base histórica de dados mais abrangente e recursos computacionais e de software para testar e comparar maior volume de dados.
No método da Média Móvel todos os períodos utilizados têm o mesmo peso dentro do modelo, ou seja, todos os períodos definidos pelo n escolhido agirão sobre o valor da previsão com a mesma intensidade.
Isto pode ser um problema em algumas situações, nas quais ao se realizar previsões, quão mais longe no passado um dado está, menor tende a ser seu alinhamento ao cenário mais atual do comportamento da demanda. Dados mais antigos podem não terem sofrido ação de forças mercadológicas que estão presentes nos momentos mais atuais, e vice-versa.
Para mitigar esta situação é possível utilizar uma Média Móvel Ponderada que irá atribuir diferentes pesos de influência aos números previstos para diferentes períodos, de modo a minorar a influência de períodos mais antigos e majorar de períodos mais novos.
Os diferentes pesos devem ser atribuídos como porcentagens (aqui representadas na forma decimal) ao total de períodos considerados de modo o total atingir 100% (ou 1 em números decimais).
Por exemplo, ao se utilizar três períodos para se realizar a previsão com Média Móvel Ponderada, se atribuiu o peso de 50% (0,5) ao período t – 1, 30% (0,3) ao período t – 2, e 20% (0,2) ao período t – 3, somando um total de 100% (1).
A fórmula para aplicação do método é a seguinte:

Utilizando o mesmo exemplo anteriormente apresentado na Média Móvel, agora irá se aplicar a Média Móvel Ponderada com os seguintes parâmetros:
· Média de três períodos com α decrescente para trás no tempo iguais a 0,5, 0,3 e 0,2 respectivamente;
· Média de cinco períodos com α decrescente para trás no tempo iguais a 0,4, 0,25, 0,2, 0,1 e 0,05 respectivamente;
· Média de sete períodos com α decrescente para trás no tempo iguais a 0,3, 0,2, 0,2, 0,1, 0,1, 0,05 e 0,05 respectivamente;
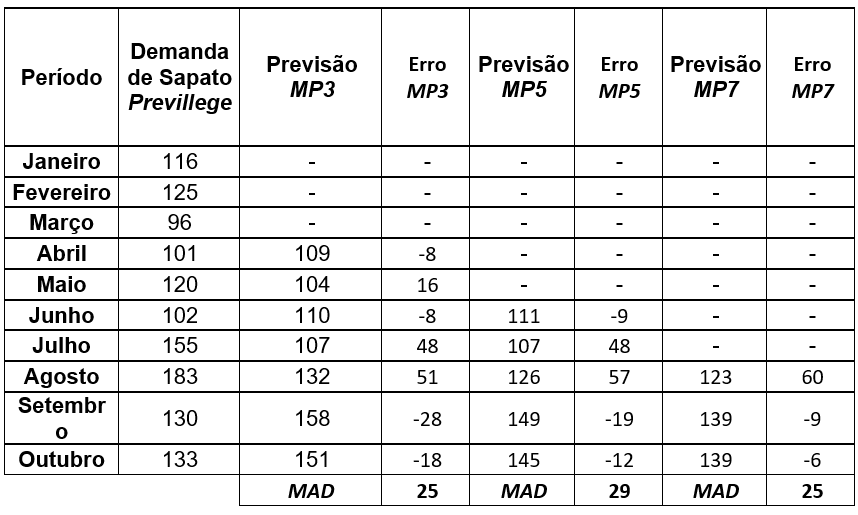
Tabela 6.5 – Previsões com MP3, MP5 e MP7

