12. Roteirização
Como mencionado anteriormente, os custos com transporte podem chegar a 2/3 dos custos logísticos, assim os esforços para melhorar sua organização e execução são imprescindíveis.
Quanto menos tempo os veículos passam em trânsito de um ponto de origem a um ponto de destino, menos custos operacionais ocorrerão (tempo, combustível, depreciação, segurança etc.), assim encontrar as melhores rotas ao longo das vias existentes impactam diretamente estes custos.
A atividade de roteirização de veículos tem uma natureza complexa e há alguns conceitos que tendem a ser seguidos ao preparar rotas sem a utilização de métodos quantitativos.
Estes conceitos não são absolutos, e estão sujeitos a inúmeras variáveis que influenciam todos os aspectos da roteirização de veículos, mas de modo geral sempre que seja possível aplicá-los, eles tenderão a trazer bons resultados. Três destes conceitos são os seguintes:
· Não cruzar rotas;
· Agrupar veículos com entregas próximas;
· Agrupar entregas em dias diferentes;
· Comece pela entrega mais distante;
· Inicie a distribuição pelo veículo com maior capacidade;
· Se há coletas a serem realizadas, insira no percurso, não as deixe para o fim;
Nunca cruzar rotas. Ao se desenvolver uma rota busca-se nunca fazer o veículo passar por pontos onde já tenha passado nesta mesma rota. Além disso as rotas devem, sempre que possível, ter uma forma que se assemelha a lágrima (ou gota).
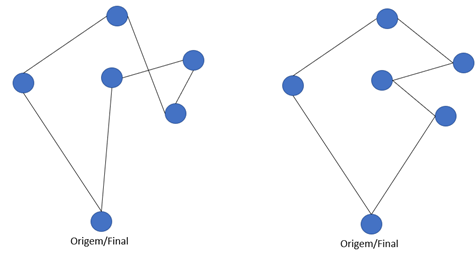
Figura 12.1 – Formato de “lágrima”
Em uma rota há cruzamentos, o que não é o ideal, na outra não há cruzamentos. Ambas têm o formato de uma “lágrima” a partir da origem.
Organizar veículos agrupando-os em viagens com entregas próximas entre si. Observe a figura.

Figura 12.2 – Agrupamento de entregas próximas
Em (a) os veículos percorrem grandes distâncias de uma entrega a outra, em (b) os veículos percorrem menores distâncias entre as entregas.
Agrupar entregas em dias diferentes. Se há roteiros a serem realizados em diferentes dias da semana, estes devem ser agrupados evitando sobreposição, observe a figura.
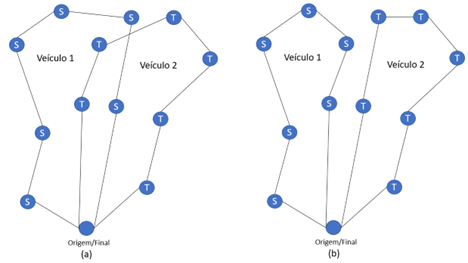
Figura 12.3 – Agrupamento de entregas em dias diferentes
Na figura os “S” se referem a entregas na segunda-feira, os “T” as entregas de terça-feira. Observe que na situação (a) as entregas de segunda e terça se sobrepõe, ou seja, não estão totalmente agrupadas. Na situação (b), as entregas de segunda e terça estão agrupadas sem se sobrepor.
Comece as entregas pela parada mais distante, a partir dela faça agrupamentos em outras paradas próximas até atingir a capacidade. Completada uma rota, identifique a parada mais longe que sobrou e agrupe outras paradas ainda não contempladas.
Tente sempre iniciar a distribuição atribuindo carga ao veículo de maior capacidade, desde que seja possível utilizar sua capacidade de forma eficiente. Nem sempre esta alternativa será viável ou possível.
Se há coletas a serem realizadas, estas devem ser inseridas nas rotas normalmente, não devem ser reservadas para o final.
A análise de rotas, além da visão espacial, também precisa levar em consideração outras características físicas dos trajetos que podem influenciar decisivamente a distribuição, o que torna esta uma análise ainda mais complexa.
Existem inúmeros métodos aplicados a resolução de problemas de roteirização, como por exemplo, quando o ponto de origem e o ponto de destino são diferentes, quando há mais de um ponto de origem ou destino, quando os pontos de origem e destinos são coincidentes, entre outros. De modo geral, dada a complexidade, estes problemas precisam ser resolvidos utilizando softwares específicos de roteirização, ou com modelagem matemática e aplicação de métodos de pesquisa operacional.
Nos tópicos a seguir serão detalhados dois métodos. Um método é bastante prático para ser utilizado em situações em que o veículo precisa realizar grande número de entregas próximas entre si (dentro de uma cidade ou região). O outro define rotas principalmente para entrega de cargas consolidadas e para grandes distâncias percorridas.
Entre os métodos comumente aplicados na prática operacional está o Método da Varredura. A grande vantagem deste método é que ele é simples e prático. Ele não trará soluções otimizadas, mas consegue organizar e aproximar as entregas com algum grau de economia.
Os passos para desenvolver o método são:
1- Com a origem e todos os destinos localizados no mapa, trace uma reta virtual a partir do ponto de origem em qualquer direção;
2- Gire esta reta em qualquer sentido (horário ou anti-horário) até que ela encontre algum destino. Verifique se o veículo tem capacidade para entregar a carga requerida ao destino, se tiver, trace uma reta da origem para este destino;
3- Prossiga girando a reta até encontrar o próximo destino. Verifique se é possível continuar entregando neste destino com a carga acumulada até agora no veículo (carga acumulada dos destinos anteriores). Se for possível ligue o destino anterior a este destino, se não for possível, finalize esta viagem retornando a origem, e abra uma nova a partir da origem;
4- Repita os passos até atender todos os destinos;
Para exemplo, considere que serão realizadas entregas na região do Sumaré na cidade de São Paulo. Os triângulos no mapa representam todos os destinos que precisam ser atendidos. Se utilizará um veículo com uma capacidade de 250kg, e que cada destino no mapa demanda 50kg, ou seja, cada viagem conseguirá atender cinco destinos.
Iniciando da origem, traça-se uma reta e gira-se ela em sentido anti-horário. Encontra-se o primeiro destino, que receberá 50kg, e liga-se a origem a ele.
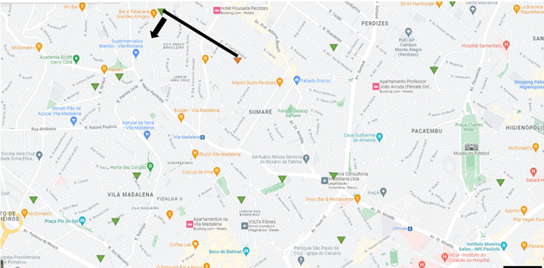
Figura 12.4 – Reta inicial
Continuando movendo a barra em sentido anti-horário, encontra-se o próximo destino que também recebe 50kg, totalizando 100kg. Liga-se o primeiro destino a ele.
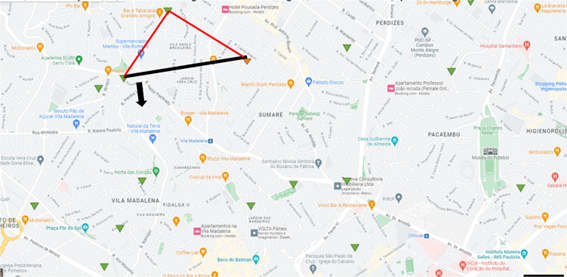
Figura 12.5 – Dois primeiros destinos
Continua-se com este movimento e ligando os destinos até atingir a capacidade do veículo de 250kg, findando assim a primeira viagem.
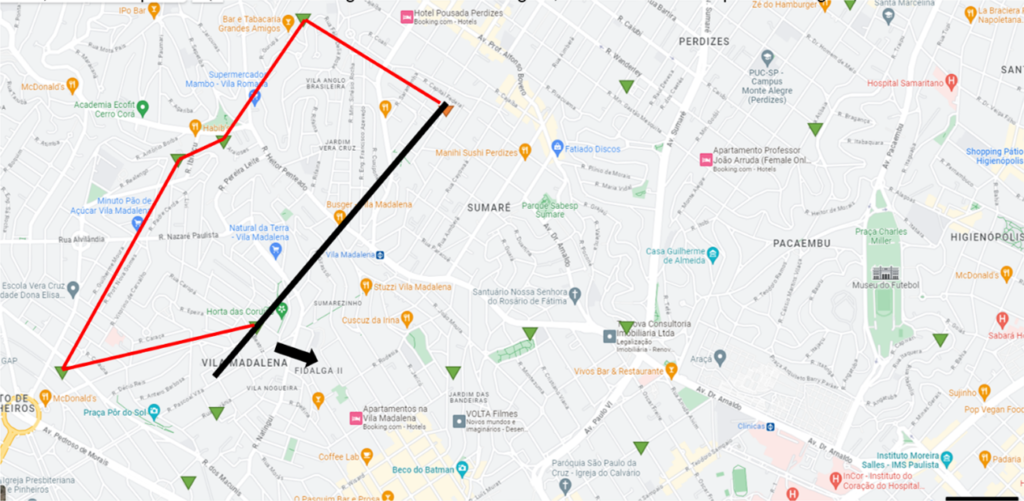
Figura 12.6 – Último destino da viagem
Prossegue-se o método até atingir todos os destinos planejados, e sempre respeitando a capacidade do veículo. O resultado das rotas será conforme a figura a seguir.
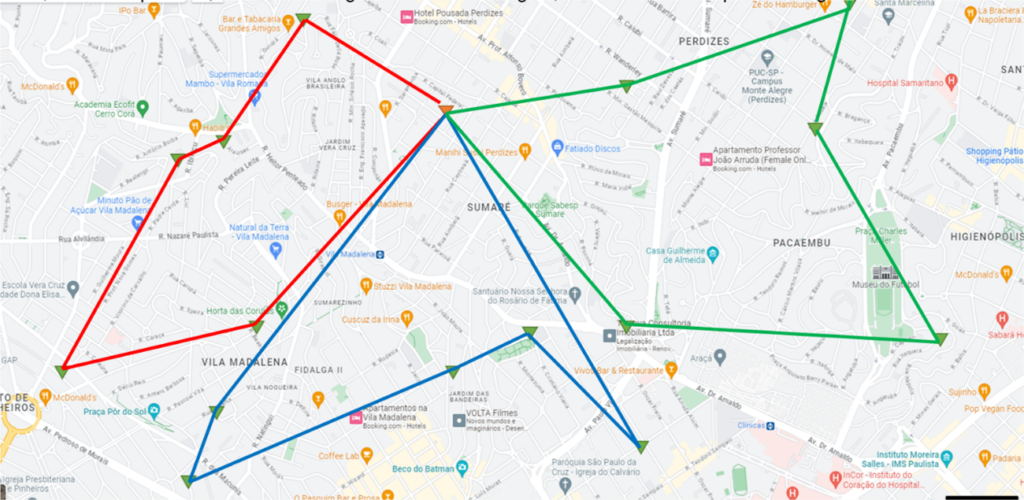
Figura 12.7 – Três viagens necessárias
O método da varredura apenas agrupa o conjunto de destinos numa mesma viagem de entrega. Depois de identificada as viagens, é preciso, sequenciá-las (geralmente seguindo o conceito de começar pelas entregas mais distantes), e determinar as rotas que serão tomadas.
A resolução de problemas de programação e roteirização torna-se mais complexo à medida que se acrescentam variáveis e limitações, o que leva a necessidade de utilização de métodos computacionais para resolução.
Estes métodos utilizam-se de programação linear e soluções heurísticas e otimizantes específicas para cada tipo de caso. Há soluções para as diferentes situações, e que envolvem invariavelmente a utilização de softwares especificamente destinados a estes tipos de problemas.
Ainda com a utilização de softwares com soluções específicas, é muito difícil encontrar soluções ótimas porque a quantidade de variáveis envolvidas em roteirizações torna difícil absorver todas elas na aplicação de um modelo.
12.2. Método do Caminho Mais Curto
Dentre as várias formas de resolução destes problemas de roteirização, será apresentado o Método do Caminho Mais Curto, que contempla a situação de uma origem e um destino, e geralmente é aplicado para entregas consolidadas de grandes distâncias. Este método aplica os mesmos princípios da técnica utilizada nos métodos PERT/CPM oriundos da administração de projetos.
Na área de projetos o método PERT/CPM são utilizados para identificar as atividades críticas, que quando atrasadas impactarão toda a evolução do projeto.
Na aplicação dentro da roteirização de veículos, será encontrado o caminho crítico mais curto que liga o ponto de origem ao ponto de destino dentro da rede. Este método é possível desenvolver de forma “analógica” sem a necessidade de utilização de softwares com programação específica para este tipo de problema.
Neste método considera-se uma rede ligada composta por nós e linhas. Os nós representam pontos de conexão entre duas ou mais linhas (que representam as vias possíveis de serem utilizadas), e as linhas representam as distâncias (ou tempo) entre os nós.
Para compreender o método, será desenvolvido um exemplo. Considere a rede com as distâncias entre os nós dadas em quilômetros, sendo A o ponto de origem, e J o ponto de destino.
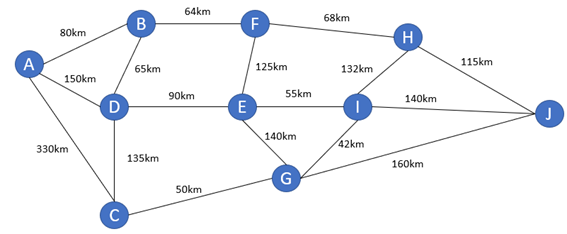
Figura 12.8 – Rede inicial
Partindo do ponto de origem A, é possível chegar aos pontos B, C e D.
Inicialmente testa-se o caminho para chegar de A até B. O caminho direto entre os dois tem 80km. Testando outros caminhos para chegar em B, nenhum apresenta uma distância menor, por exemplo, seguindo de A para D, e depois para B, soma-se 150km + 65km resultando em 215km.
O caminho direto é mais curto. Testando outros caminhos para chegar em B, também sempre se terá uma distância maior, assim o caminho mais curto entre A e B será o caminho direto entre eles.
Partindo para o caminho mais curto entre A e D, tem-se o caminho direto que tem 150km. Testando outro caminho, indo de A para B, e em seguida para D, soma-se 80km + 65km, um total de 145km. Este caminho é mais curto que o caminho direto entre ambos, assim será excluído o caminho direto.
Testando outros caminhos para se chegar em D, nenhum será menor que o caminho A-B-D. Veja como fica a rede até o momento, com a exclusão do caminho direto A-D (que é mais longo).
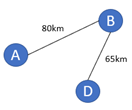
Figura 12.9 – Ligação A-B-D
Prosseguindo a análise, verifica-se o caminho mais curto de A para C. O caminho direto tem 330km, verifica-se se há outro caminho mais curto. O caminho A-B-D-C (80km+65km+135km) tem 280km, ou seja, é menor que o caminho direto, assim, exclui-se o caminho direto A-C. A rede tem um total acumulado de 280km até agora, e é representada a seguir.
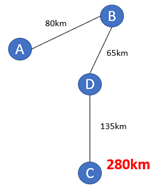
Figura 12.10 – Ligação A-B-D-C
Já se testou todos os caminhos a partir de A, deverá se repetir o procedimento a partir dos novos pontos disponíveis B, C e D.
Agora partindo de B, testa-se todos os nós que ele atinge, que no caso é somente F. O caminho direto tem 64km, outro caminho alternativo, seria B-D-E-F (65km+90+125km) que tem 280km.
Assim, pode-se excluir o caminho que liga E a F, porque há outro caminho (o caminho direto de B para F) para F que é mais curto, este caminho não tem relevância. Nenhum outro caminho de B para F é menor que o caminho direto entre eles, então este caminho permanece. O caminho acumulado A-B-F está em 144km.
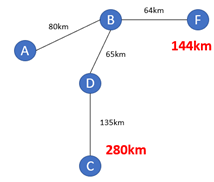
Figura 12.11 – Rede com duas rotas possíveis
Agora a partir de D, analisa-se todos os nós que ele encontra, que são C, que ele já está ligado devido aos passos anteriores e E.
O caminho direto de D para E tem 90km, outro caminho possível para ligar ambos seria, D-C-G-E (135km+50km+140km) com 325km, que é mais longo. Assim, pode-se excluir o caminho que liga G-E, porque outro o caminho direto é mais curto. Assim o caminho direto é o mais curto.
A partir de C, os nós que ele atinge são D, que já está ligado, e G. O caminho direto C-G tem 50km, outro caminho seria C-D-E-G (135km+90km+140km) com 365km, outros caminhos são mais longos, então permanece o caminho direto.
Os caminhos completos e disponíveis até aqui são A-B-F com 144km, A-B-D-E com 235km, e A-B-D-C-G com 330km. Por enquanto a rede está assim.
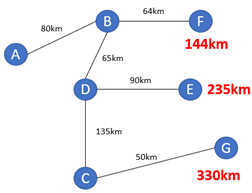
Figura 12.12 – Rede com três rotas possíveis
Partindo de F, liga-se a H com 68km. Como o caminho de F para E já foi excluído, outros caminhos também não levarão a uma distância menor. O total desta rota A-B-F-H está em 212km.
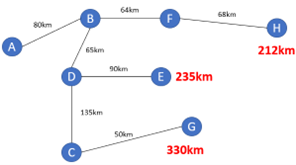
Figura 12.13 – Ampliação para a rota F-H
A partir de E, liga-se I com 55km. Como o caminho E-G já foi excluído, outros caminhos também não levarão a uma distância menor. O acumulado deste caminho está em 290km.
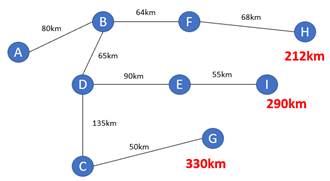
Figura 12.14 – Ampliação para a rota E – I
A partir de G, liga-se também a I. O caminho G-I tem 42km, que acumulando com os 330km percorridos até agora daria 372km. Mas chega-se a I, com o caminho que vem de E, com um acumulado de 290km. Ou seja, chegar até I vindo de G, é mais distante, assim esse caminho pode ser excluído e a rota a partir de G não prossegue.
Agora sobram H e I para ligar a J que é o destino. Partindo de H que já tem um acumulado de 212km, e somando 115km, chega-se a J com um acumulado de 327km. Partindo de I, que tem um acumulado de 290km, somando-se 140km, tem-se um acumulado de 430km.
Assim, a ligação mais curta será a partir de H com um acumulado de 327km, ficando a rede conforme apresentado na figura 50.15.
O método então determinou que o caminho mais curto de A até J é A-B-F-H-J com 327km. Não há outro caminho mais curto, assim este deveria ser o caminho tomado para ligar a origem ao destino.
Neste exemplo utilizou-se quilômetros para mostrar as distâncias entre os nós, mas também pode-se usar o tempo.
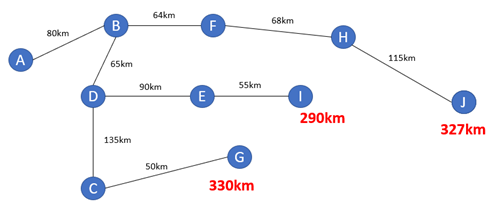
Figura 12.15 – Rota final
Esse tipo de problema também pode ser resolvido com o Microsoft Excel, softwares de modelagem matemática e estatística, ou com softwares que tenham soluções direcionadas a roteirização.
