11. Distribuição de cargas
Como já mencionado, o modal de transporte mais utilizado é o rodoviário principalmente em função da sua flexibilidade e acessibilidade. Assim, aqui será abordado um método de otimização que pode ser aplicado para diversas situações dentro da administração, e no caso dos transportes funciona muito bem para distribuição de cargas fracionadas por meio rodoviário, mas pode ser utilizado em qualquer situação.
A distribuição de cargas é a atividade de designar veículos, com cargas para os clientes onde estas precisam ser entregues. Geralmente no caso de entregas regionais, nas quais não são entregues cargas cheias, consolidadas (toda a carga entregue em um único local), e se trabalha com cargas fracionadas (um veículo entrega uma parcela da carga em vários locais), é preciso determinar quais veículos entregarão quais materiais em quais locais.
Ao administrar uma frota de veículos, é preciso determinar que num dia qualquer de trabalho, por exemplo, o veículo A irá entregar 100 unidades do produto X para o cliente Z, ou que o veículo B irá entregar 200 unidades do produto H, para o cliente Y. Num ambiente com certa variedade de produtos e com mais de um veículo na frota, a tarefa de planejar esta distribuição pode-se tornar bastante complexa.
Considerando uma pequena frota de três veículos, que entreguem uma gama de 20 produtos diferentes para 50 clientes, tem-se um cenário complexo que pode apresentar inúmeras formas diferentes de realizar as distribuições diárias.
Como sempre, os métodos vinculados a logística buscam realizar suas atividades de modo a atingir economias, mas sem que o serviço seja prejudicado. Considerando o exemplo dado anteriormente, cada forma diferente que seja arranjada para as distribuições apresentará um custo diferente para a empresa.
Para exemplificar, considere a situação em que se tem três veículos (A, B e C) com capacidade de carga diferentes, e são usados para realizar entregas. Há necessidades diferentes a serem atendidas nos destinos D1, D2 e D3, sendo que a designação de um veículo para um local diferente tem um custo por unidade também diferente.
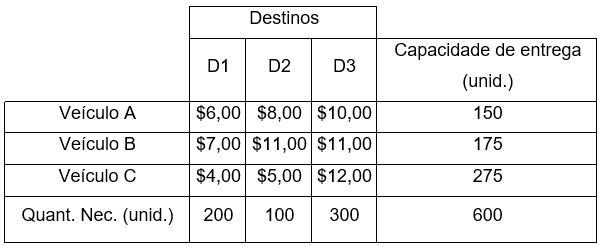
Tabela 11.1 – Exemplo de custos de uma distribuição
O cruzamento entre o veículo e o destino apresenta-se o custo unitário da entrega. Por exemplo, para o veículo B entregar no destino D3 há um custo de $11,00 por unidade.
Observe que é possível fazer inúmeras combinações de entregas de veículos com quantidades variadas aos destinos.
Considere um exemplo arbitrário qualquer onde o veículo B tem uma capacidade de entrega de 175 unidades, o destino D3 tem uma necessidade de 300 unidades. Para atender o destino D3, se o veículo B entregasse toda sua capacidade de 175 unidades, ainda faltariam 125 unidades que deveriam ser atendidas por outro Veículo.
Imagine que o veículo A realize esta entrega restante da necessidade de D3, ter-se-ia a seguinte distribuição.
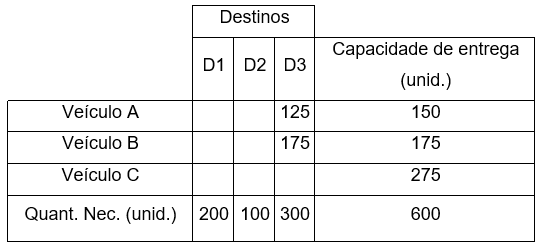
Tabela 11.2 – Distribuição aleatória
Foram apagados os custos na tabela e deixado apenas as quantidades a serem entregues pelo veículo B e A no destino D3. Os dois veículos entregando atingem a quantidade necessária de D3, e levaria a um custo de entrega em função dos custos apresentados na tabela 49.1 de:
Veículo B = 175unid x $11,00 = $1.925,00
Veículo A = 125unid x $10,00 = $1.250,00
Total = $1.925,00 + $1.250,00 = $3.175,00
Apenas para atender a necessidade de D3, utilizando-se dos veículos A e B, iria se incorrer num custo de $3.175,00.
A necessidade de D3 foi atendida, mas ainda falta atender os destinos D1 e D2. Prosseguindo no exemplo, determinou-se o restante das entregas de modo a atender todos os destinos e utilizar a capacidade dos veículos. Considere que a distribuição final ficou da seguinte forma.
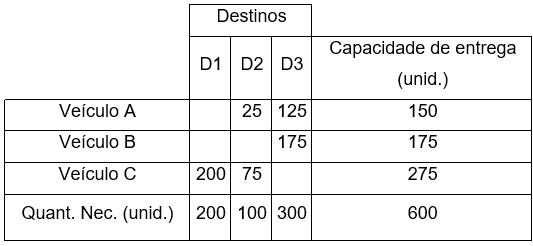
Tabela 11.3 – Distribuição aleatória final
Baseando-se nas quantidades entregue por cada veículo e o custo unitário mostrado na tabela 49.1, realizar a distribuição desta forma levaria a um custo de $4.550,00.
Perceba que esta é apenas uma forma entre várias possíveis de se realizar estas entregas. Se poderia variar a forma de distribuição dos veículos aos destinos de diversas formas diferentes. Cada forma que for simulada levaria a um custo diferente, alguns mais altos outros mais baixos.
O desafio está aí, se cada arranjo simulado levaria a um custo diferente, e sabendo que apesar de ser possível realizar esta distribuição de diferentes formas há um número finito de possibilidades, logo, haverá uma forma de realizar a distribuição que levaria a um menor custo total.
Para tratar deste tipo de problema existem algumas ferramentas vinculadas a estatística e pesquisa operacional. Normalmente ao se utilizar este tipo de ferramenta se atingirá um resultado ótimo, ou seja, um resultado que diante dos dados não haverá outro com melhor desempenho, ou ainda um resultado sub-ótimo, mas que entrega um bom desempenho.
Para resolver este problema de distribuição com cargas fracionadas em diferentes destinos, aqui será apresentado o método utilizando o recurso Solver do Microsoft Excel.
11.1. Resolvendo o problema de distribuição com o Microsoft Excel
A ferramenta Solver do Microsoft Excel é utilizada para modelagem e resolução dos mais diferentes tipos de otimização.
Este recurso não vem habilitado no Excel, assim o primeiro passo é realizar sua ativação. O caminho para ativação pode mudar a forma de uma versão para outra do software, mas de modo geral segue este formato.
Com o Microsoft Excel aberto, clique na aba “Arquivo”, e se abrirá o seguinte menu.
Figura 11.1 – Menu “Arquivo”
Clique em “Opções” ao final. No próximo menu, selecione “Suplementos”, na linha “Ferramentas de Análise” e clique em “Ir”.
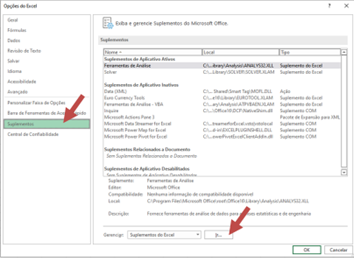
Figura 11.2 – Menu “Suplementos”
No menu seguinte, selecione “Ferramentas de Análise” e “Solver”, finalizando com “OK”.
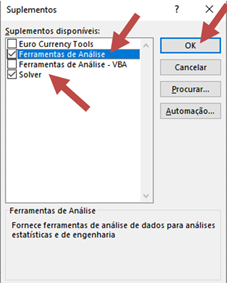
Figura 11.3 – Menu de habilitação
Depois de processar por alguns instantes, e talvez pedir para reiniciar o Microsoft Excel, a ferramenta foi habilitada.
Na imagem a seguir é apresentada numa planilha do Microsoft Excel a matriz de custos da situação exemplificada no início do capítulo, e uma cópia dela sem os custos.
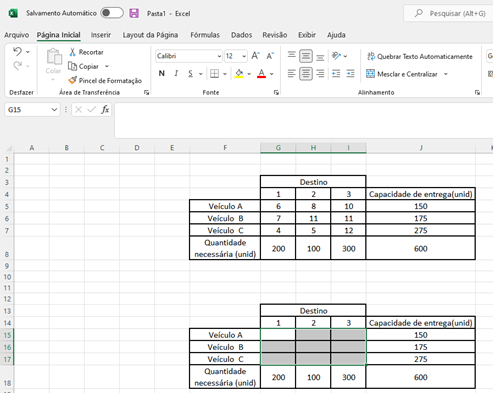
Figura 11.4 – Estrutura inicial
Numa célula relacionada ao custo da solução, será inserida a fórmula “SOMARPRODUTO”. Na fórmula será referenciada as células da matriz superior (G5:I7), onde estão os custos, e as células da matriz inferior (G15:I17), que estão vazias.
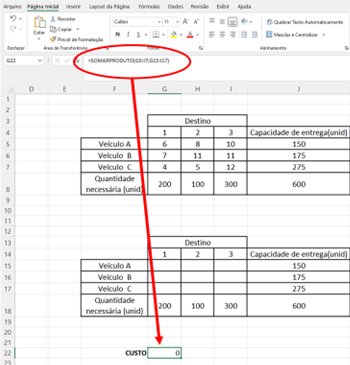
Figura 11.5 – Fórmula para o custo total
Adiciona-se uma linha nomeada “RECEBIDA” e uma coluna nomeada “ENVIADO”. Na célula G19 adiciona-se a fórmula “SOMA” considerando as três células vazias da coluna 1 (G15:G17). Repete-se esta fórmula para as células vazias da coluna 2 e 3.
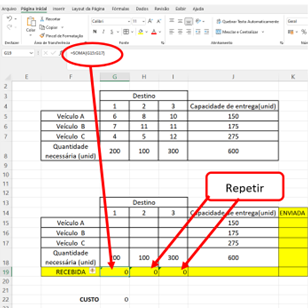
Figura 11.6 – Fórmula nas colunas para as restrições
Na célula K15 adiciona-se a fórmula “SOMA” considerando as três células vazias da linha do veículo 1 (G15:I15). Repete-se esta fórmula para as células vazias das linhas dos veículos 2 e 3.
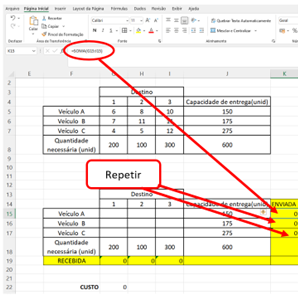
Figura 11.7 – Fórmula nas linhas para as restrições
Acesse a aba “Dados” e depois o botão Solver. No menu que aparecer, no campo “Definir Objetivo”, referencie a célula com a fórmula do custo (G22).
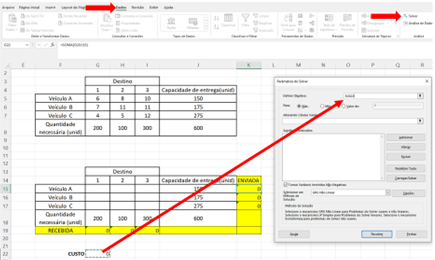
Figura 11.8 – Função objetivo
Selecione o ícone “Min” e altere o método de solução para “LP simplex”, e desmarque o item “Tornar Variáveis Irrestritas Não Negativas”. No espaço “Alterando Células Vazias” selecione as células vazias da segunda matriz (G15:I17).
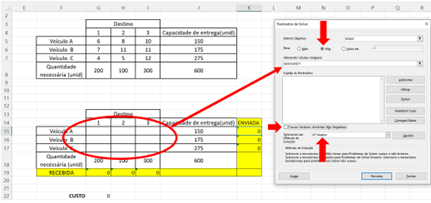
Figura 11.9 – Indicação de Minimizar e Células variáveis
O próximo passo é o mais trabalhoso que é inserir as restrições. Clica-se no botão “Adicionar” que abrirá uma nova janela onde será indicado três entradas diferentes. Primeiro, deve-se indicar no espaço “Referência de célula” a célula G19, no próximo espaço seleciona-se “=”, e no espaço “Restrição” referencia-se a célula G18. Ao terminar estas indicações clica-se no botão “Adicionar”.
A janela volta a ficar sem indicações. Deve-se repetir este processo para o par de células H19 e H18, “Adicionar”, e para I19 e I18, “Adicionar”.
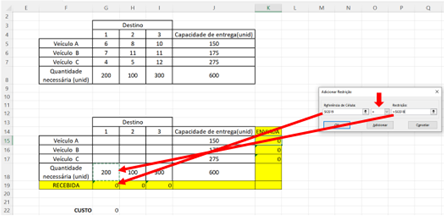
Figura 11.10 – Restrições da coluna
Realiza-se o mesmo processo com os pares de células: K15 e J15; K16 e J16; K17 e J17. Sempre indicando o sinal “=” e clicando em “Adicionar” ao final de cada par de células.
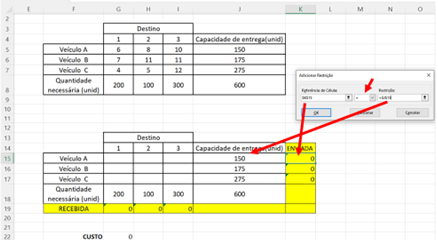
Figura 11.11 – Restrições das linhas
O próximo passo é adicionar a restrição de não negatividade. Em “Referência de Célula” seleciona-se o conjunto de células vazias G15:I17. Na janela de sinais, selecionar o sinal maior ou igual “>=”, e em “Restrição” digitar o número zero “0”. Em seguida clique em “Adicionar”.
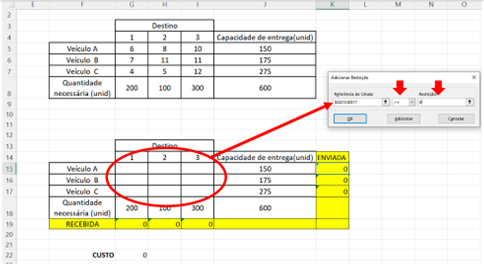
Figura 11.12 – Restrição de não negatividade
Depois de adicionar esta última restrição clique no botão “Cancelar”. A janela inicial aparecerá novamente e clica-se em “Resolver”.
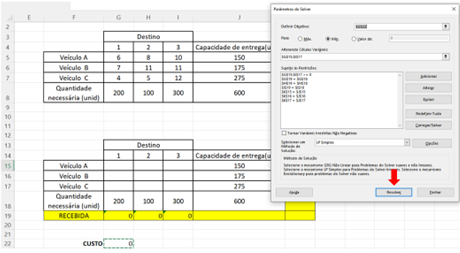
Figura 11.13 – Resolver
O Microsoft Excel irá resolver o problema e indicará a frase “O Solver encontrou uma solução. Todas as restrições e condições de adequação foram satisfeitas”. Nesta janela deve-se clicar em “OK”.
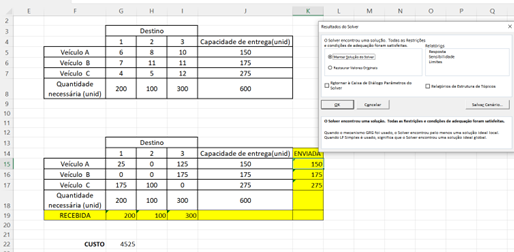
Figura 11.14 – Resolução
Observe que foi definida uma distribuição automaticamente nas células que estavam vazias. O Veículo A deverá entregar 25 unidades no Destino 1, e 125 no Destino 3, atingindo sua capacidade de 150 unidades, e assim para os outros veículos também. Com todas as distribuições definidas, o custo total final ficou em R$4.525,00.
Em função dos dados disponibilizados, esta distribuição será a distribuição ótima que levará ao menor custo total possível. Talvez haja alguma outra distribuição que leve também a este mesmo custo total mínimo, mas nenhuma outra forma conseguirá atingir menores custos totais.
